itch.io

YouTube raczyło nam kilka dni temu pokazać trailer, poczekaliśmy na premierę i postanowiliśmy zagrać. Jak na grę tej kategorii, zaskakująco dobre! Rozwiązywanie problemu szamba nas zachwyciło.

If you are in the version downloaded here (13.0a), and activate as explained above (not some other way, i.e., not by loading the portalscene3.lev file directly), you should be able to rotate the camera with WASD and move with IJKL.

RogueViz Collection on Steam should work on Mac natively. We have not yet added information about OSX support to the Steam Store because it is not tested sufficiently yet. On our Mac, the starting animation crashes (that can be circumvented by adding launch option `rv_startviz=0`), but that is probably because it is a very old Mac.

I encountered a crash in the following situation:

Drop 17 items in the same spot. Press 'g' to pick up. Since there are 17 items and the menu shows only 16, you need to press down to see the last item. After that, press any key from 'a' to 'p', and the game crashes.

There is also an issue in the shop inventory that, when the shop has lots of items, pressing keys from 'q' to 'z' selects items from the second page even though such letters are not assigned on the screen -- which is especially wrong for the  'z' key which is listed on the screen as the "exit" key.

And unidentified weapons and armor still display their damage/armor values in the 'i' screen sidebar.

I have enabled the cheat mode to reproduce the crash quickly, so I have some comments on the cheat system. "Revive" should probably fix starvation, and probably also poison/bleeding/etc. It might be good to display a warning if the player selects "accept your fate" when already cheating (especially that it deletes the save file -- another solution is to ask about this deletion).

The main idea for RogueViz collection was to make the games available to people who prefer to play games on Steam -- the games are available on itch.io as individual games. (While idealistically itch.io is better, I generally prefer people to buy my games on Steam than on Itch since I believe it makes them more visible, especially with a review.)

Although their versions in the RogueViz Collection are improved -- more specifically:

• they have online leaderboards and achievements (these are only possible on Steam)
• it is a single executable in which you pick the specific game from the main menu which might be more convenient
• some new levels in Nil Rider (which have not yet been added to the itch.io version)
• NilRider/Bringris have a "star" system which unlocks more complex levels after finishing the basic ones
• the online version Seuphorica  is only square grid while the RVC one allows non-Euclidean, and also they have different interfaces
• some bugfixes and other minor improvements
• probably more in the future

So I was not planning to make an itch.io version, but I guess I could make one.

One player in the HyperRogue discord has fixed the green lines issue by updating their GPU drivers, and changing the GPU used by the game (in the operating system graphics settings).

Thanks for the report! This should be fixed in 1.1.

Both the interface (on abstract level) and the procedural generation were innovations of Rogue. Rogue even has a section  of the manual  which explains how was it different from other games, and it mentions both. Some sources say Rogue was the first graphical adventure game. When "roguelike" got official in 1993 (and also earlier), it was about the interface, not the procgen. The genre was not called e.g. "ASCII dungeon" because they realized that neither using ASCII or the dungeon was important. There were games before it  (like Beneath Apple Manor which had both aspects) but it was Rogue which inspired them.

Electro-Mechnician is not an action game (that means games emphasizing physical challenges) and not really a dungeon crawler (no exploration, no loot, no traps, etc., and some people say that dungeon crawlers are the 3D ones...). There are lots of procgen/randomized games which do not appear to be inspired by Rogue. Games where you move and fight like in Rogue but not procedurally generated are very rare, please tell me if you know some interesting ones. (Kroz and Ultima are not that similar, maybe DROD but that is more of a puzzle than adventure.) 

Wow, a non-randomized roguelike! These are rare, especially good ones.

Very cool! I thought it would be another game in the recent ocean of Balatro-like "something + engine building", but it is more like Desktop Dungeons.

The Chinese translation has been added quite recently, and the Android version has not been updated since then.

Currently the boxes close to the center are very narrow and the boxes far away are very wide. You could use a conformal projection to prevent that (basically map the radial coordinate r using exp(k*r) for some k).

Thanks! Blue and red squares only affect Red/Blue tiles (which is quite significant IMO).

How do boons work? I got "ixchel" and "enki" but I do not see any tiles getting better or extra points stamps.

(I was looking for existing Scrabble deckbuilders before writing Seuphorica, but I could not find this one... seems to be a quite different take, though!)

Seuphorica ( https://zenorogue.itch.io/seuphorica ) seems to be have some things you want :)

A roguelike is a game where you move like in Rogue, and this is just a list of features that roguelike players enjoy, with some omissions and some badly formulated, that was mistakenly assumed to be a definition. Canonical roguelikes rarely satisfy "Monsters are similar to players" or non-modality by the level of strictness you are expressing here.

IMO "non-modality" just means that there is no separation between exploration and combat (as opposed to e.g. typical JRPGs), so you should get full score despite the Shrine mini-games. And 0 for "monsters are similar to players" would be something on the level of mines in Minesweeper.

Should be fixed now -- it seems I have uploaded the old version again to itch.io. 

Thanks for the report! Should be fixed.

Thanks! I have forgotten to disable the Itch.io checkbox which disables scrollbar, should be fixed now.

Thanks!

For those who do not want to share their code publicly (but be included in the statistics), there is the suggestions form.

Not sure which justifications you consider vague -- probably opinions like "Spelunky/Isaac is not a roguelike because it is not turn-based" should be mentioned, since they are said quite frequently and not vague.

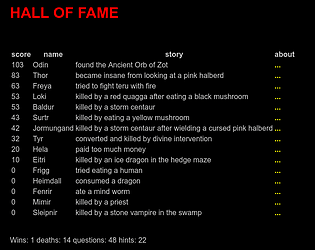
Thanks! Here are the early aggregate results (based on the first 13 votes posted here, via the in-game form, on Twitter or Discord servers): https://twitter.com/ZenoRogue/status/1768665726011711511

Thanks! You can click "details" to see how these are defined. Spatial is intended to be a looser variant of "grid-based": the combat takes place in some space with relevant geometry, but it can be continuous. Text adventures, JRPG-style, card battle combat typically violates this. There are some games which are quite close to traditional roguelike but not strictly grid-based (e.g., billiards roguelikes,  Rootin' Tootin' Lootin' Shootin').

Thanks!

Agreed, the information about meta in Slay the Spire was indeed misleading, reformulated it to be more precise.

Thanks!

This was mentioned as "META same world", but added this in "controversies" too. (Also the meta violations was not given correctly for DF.) From the games not in the quiz, AFAIK CataclysmDDA and Unexplored II also have an option to play in the same world.

It is not planned at the moment. Our MacBook is quite old. We can compile HyperRogue on it and AFAIK it still works on newer MacBooks, but to upload a new version to iOS AppStore, it forces us to update XCode, which forces us to update OSX, which forces us to get a new MacBook. So this platform is not very friendly for those who are not very invested in it. I have seen some other cool non-Euclidean-ish games that were iOS-only and are no longer available :(

If you mean "Portals to non-Euclidean Geometries":

* "rogueviz demos" in the menu

*   portal collection

* press Enter a few times until you get to "inter-geometric portals", or alternatively, press '9' and select it from the menu

* click "run this visualization" (note: may take some time to compile the shader)

Does this help?

The source code of RogueViz should be possible to compile quite easily in Linux (we work mostly in Linux ourselves).

Thanks for the nice words and the nice review!

Unfortunately, I have not seen this reported by other people, so I am not sure whether I am able to help :( Some ideas:

- are your graphics drivers up to date?

- you could try running with commandline option `-O0' -- which disables OpenGL.  But most visualizations will not work with OpenGL, and the others will be much slower, so this is more a method to gather more information than a solution.

- what graphics card and operating system are you using?

Thanks for trying!

You mean the itch.io app? I think it did download the game (if you somehow played the web version via the app, it would be less smooth too).

On my computer, in itch.io app, Library -> installed items -> Bringris -> [cog icon] -> "manage" -> "show in file manager" and you should see the files on your computer, and you could try running it directly, or see if you have a file "bringris.ini" that you could try to delete.

Thanks! There was no update recently, so it must be either bad configuration (you could try finding and deleting the file bringris.ini) or something has changed in your system. Does it launch not from the itch browser?

Any specific issues, and what VR headset are you using?

I run SteamVR, and then in RogueViz, enable VR in settings -> 3D settings -> VR settings.

I would like to draw attention that USA is not the only country which has recently restricted access to abortion -- supporting American women but not supporting e.g. Polish women does not feel perfect to me. The bundle contains games from people around the world and will be bought by people around the world.

Thanks!

Yeah, some of the trophies are probably hard -- the times are based on a computer solver, who sometimes finds ways to cut off time that I was not expecting. (Although a few seconds over the solver's solution are allowed.)

Nil is homogeneous (the same at every reference point) but anisotropic (not the same in every direction). Although it is rotationally symmetric (the up/down direction is special, but you can rotate around this axis).

No idea about actual planets :) I do not think anybody has studied that.

Thanks for playing!

After crashing into a castle or running into edge, you can reverse the time (the default key is 'b') or restart the game.

If you collect the four triangles fast enough, you win. (The first track has two goal times, one should be very easy, and the other one should be very hard.) Then you can go to another track in the menu. (Other tracks have different shapes, and also their goals are sometimes different than "collect all the triangles fast enough".)

Yeah, usually "negative" qualifiers in mathematics mean some specific things. "Irrational number" does not mean numbers like i or Aleph-Zero even though they are not rational numbers. It means a *real* number that is not rational. Discovery of such numbers was quite important in math. Same as with non-Euclidean geometry, the discovery that all the axioms could be satisfied but not the fifth one was important again. So it originally meant just that, not satisfy the 5th but satisfy all the others. Some people extend this but they usually try to keep the spirit (hard to explain Nil geometry using axioms, but the spirit of  parallel axiom is no longer there...). Sometimes "non-X Y" is meant to include "X Y" as a special case :)

Anyway, thanks for the nice game! I have added a mention to my article.

Fixed, thanks! Addresses automatically converted to links and then still pointing bad to wrong stuff when the address is edited are annoying :/

I see the point about the platform returning to the same location after going around the hole, it is indeed a bit similar to would happen in the universal cover. However, IIRC if you move the platform A, go around the hole to find a yet unmoved platform, and then go back, the platform A also becomes unmoved, so it is still not really the same thing...

I would say that the parallel axiom is not violated (the spirit of this axiom is that parallel lines behave weirdly, they converge/diverge, or in 3D they could also twist -- since the gravity is preserved in most of the game, the gravity lines act like normal parallel lines, same with the lines orthogonal to them.). The only place I have found so far where gravity lines cross (in some sense) is the "sphere" level.

> Furthermore, from Euclid’s axioms, it follows that a line segment is the shortest path between two points, which is absolutely untrue in all “R^n with portals” worlds due to a trivial counterexample.

I would not agree with this, because by this logic, any L-shaped level is non-Euclidean because the shortest path is not straight.

It is still piecewise straight, so we should allow for piecewise straight lines here, and in portal spaces shortest paths are again piecewise straight lines (well, unless the obstacles are curved).

Also this is not really a property of non-Euclidean geometry -- shortest lines are straight lines in all classic non-Euclidean geometries.

(again, in both cases the weirdness happens due to topological rather than geometrical effects)

I do not think "non-Euclidean geometry" is that common, mostly they say just "non-Euclidean" without geometry (one thing contributing to the confusion is CodeParade's "non-Euclidean worlds" viral video, he thinks that "non-Euclidean geometry" should not be used for any weird space but just "non-Euclidean" is fine -- this makes some sense but it still confuses people so I do not agree with him). "Impossible space" is what most people who care say. Thanks for considering this!

No (RogueViz is free so it is not applicable).

Seems you are confusing geometry and topology here and in the description on GitHub... (geometry is a local property that is changed when you stretch the space and topology is changed when you cut/glue the space -- portals change the topology, not the geometry; in the "sphere" level you have the topology of the sphere but the geometry is Euclidean, not spherical. The geometry is Euclidean everywhere, at least from what I have seen so far)

Also not sure why you say it is "the universal cover of a massively twisted space"? This does not seem to be accurate either. (From this description I would expect a world in the shape of e.g. an annulus that always looks like an annulus, but the contents are different when you go around the hole -- this would be the cover of the annulus, and if you never go back no matter how many times you go around, that would be the universal cover (it is more fun with two holes as you get the full binary tell then); here, the walls also sometimes all change when you go around a hole)

A bit similar 2D portals were used in the 7DRLs by Jeff Lait (Jacob's Matrix was the first one IIRC and Vicious Orcs was another one), although he did not do that much with this concept.