Both!
We like to think they're about equal in utility! Both have a base at-will instakill chance of 16.7% (10+ on a 2D6 roll and a given number on a 1D6 roll both come out to 16.7%). CUT lets you roll another possible instakill to counter incoming damage, but your chance to counter diminishes as incoming damage outscales yours. TECHNIQUE only lets you roll once but can be cheesed with WAR DICE (unlike CUT), since you're trying to exceed rather than match a target number.
If you don't produce WD or gain them frequently through advancement, CUT is likely the better choice for an instakill ability, but your chance to instakill caps out at roughly 33.3% assuming the best possible circumstances (you attempt both an at-will and counter instakill, damage range matches enemy's exactly, access to a cutting weapon, ability to handle incoming damage if your counter misses). If you want a more reliable, less risky instakill, TECHNIQUE can be boosted up to a whopping 62.5% chance with the addition of a WAR DIE and works without a weapon or the risk of taking damage if you fail (your damage simply whiffs instead).
EDIT: CUT's counter chance actually also diminishes if the enemy has a lower damage range, or if you and the enemy have matching damage ranges that use more than 1D6 (e.g. 1D6 vs. 1D6 has a 16.7% chance to match, but 2D6 vs. 2D6 has only about 11.3% chance to match).
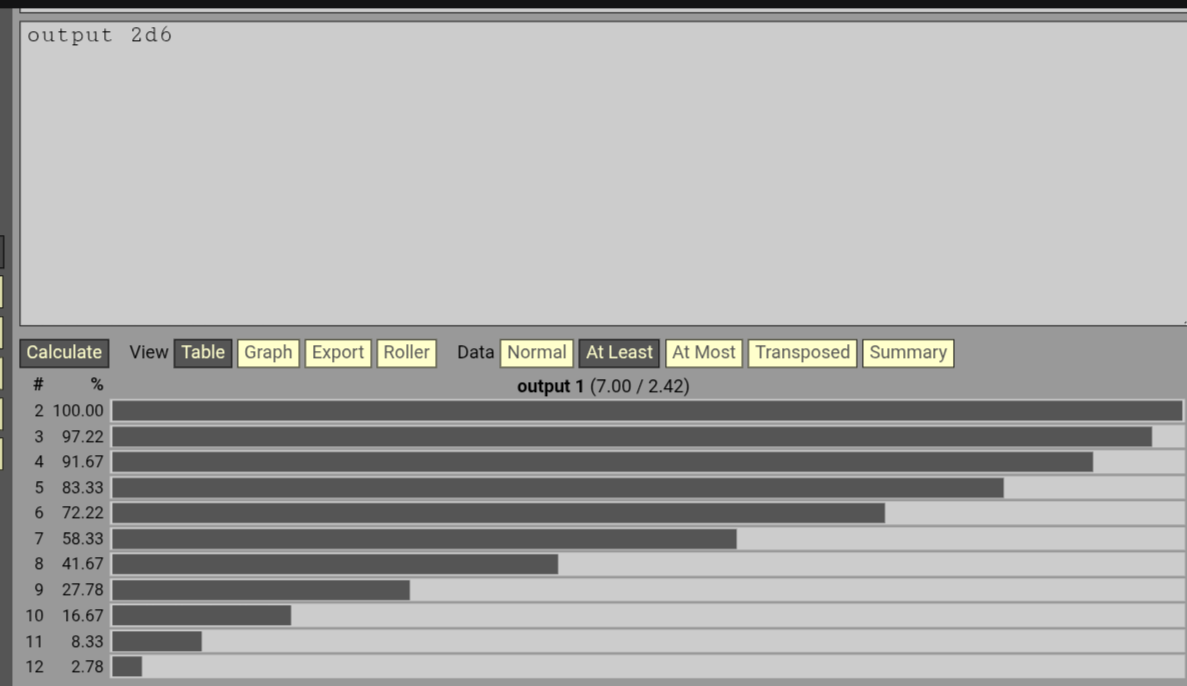
According to https://www.anydice.com/ , +10 on 2d6 has 8.33% chance against the 16.67% chance of a single number on 1d6. However, I do admit that I hadn't thought about the WAR DICE usage on TECHNIQUE.
8.33% is the chance of rolling a 10 exactly! If you switch the Data option from "Normal" to "At least", you'll see the probabilities for rolling equal to or above a given number. The cumulative probabilities of rolling 10, 11, and 12 (8.33, 5.56, and 2.78 respectively) add up to 16.67 - or 16.7, if you wanna round it.
It's possible we've made a mistake on Anydice (and if so, thank you for pointing out a balancing error in the game), but these results seem to check out: