I'm targeting the spec of XO-CHIP, and I put speed restriction aside. And somehow I got myself too busy IRL, which I don't really think I can complete it for this Jam. But I'll try to put some ideas I'm using achieving the goal of the development...
Kouzerumatsukite
Creator of
Recent community posts
Alrighty, I had multiplication routine on me, and I'm sharing it with sincere here 😊
The routine here follows peasant multiplication algorithm.
The principle is same long multiplication method, which is usually taught on school
The primary multiplication routines
This is the most crucial part for performing multiplication, summing multiplicand to product for every bit of multiplier:
# Per-bit mult sum, primary component of 8-bit mult : mul_bit v2 <<= v2 v3 <<= v3 v2 |= vF v1 <<= v1 if vF != 0 then v3 += v0 v2 += vF ;
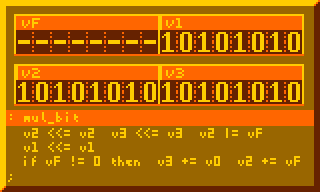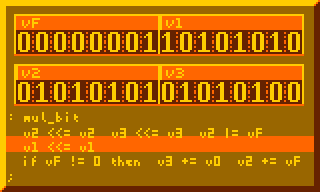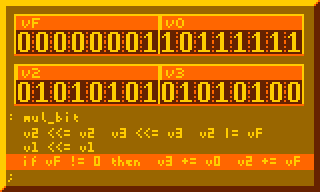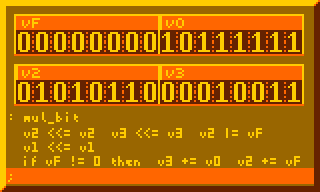
The subroutine above executed 8-times in the 8-bit multiplication routine below:
#################################################### # Full 8-bit multiplication routine (primary) # 8-bits operands, with 16-bits product # | v0 | OPERAND A 0x12 # | v1 | OPERAND B 0xFF # |======= X | =v2===v3= X # | v2 v3 | RESULT 0x11 0xEE #################################################### : mul8p # Initialize v2 := 0 v3 := 0 # Multiply! mul_bit mul_bit mul_bit mul_bit mul_bit mul_bit mul_bit mul_bit ;
[there is no illustration for this, as creating the animation is pain af]
And yes, 8-bit multiplier, takes both operands in 8-bits, gives 16-bits products.
The first 8-bit of the product is high-byte, the latter 8-bit of the product is low-byte.
Thus, this would be the building blocks to perform 16-bits or 32-bits multiplications. 😄
Alright, there are another primary multiplication subroutines out of the full 8-bit multiplier.
A full 16-bit multiplier!
##################################################### # Full 16-bit multiplication routine (primary) # 16-bits operands, with 32-bits product # | v0 v1 | OPERAND A 0x12 0x34 # | v2 v3 | OPERAND B 0xFF 0xFF # | ============= * | =v4===v5===v6===v7= # | v4 v5 v6 v7 | RESULT 0x12 0x33 0xED 0xCC ##################################################### : mul16cro # Carry out v6 += v3 v5 += vF v4 += vF v5 += v2 v4 += vF ; : mul16p # Backup operands i := multmp0 save v3 # Multiply matching parts i := multmp0 load v2 v1 := v2 mul8p v4 := v2 v5 := v3 i := multmp1 load v2 v1 := v2 mul8p v6 := v2 v7 := v3 # Multiply across parts i := multmp0 load v3 v1 := v3 mul8p mul16cro i := multmp1 load v2 mul8p mul16cro ;
aaaand a full 32-bit multiplier:
#################################################################################### # Full 32-bit multiplication routine (primary) # 32-bits operands, with 64-bits product # | v0 v1 v2 v3 | OPERAND A 0x12 0x34 0x56 0x78 # | v4 v5 v6 v7 | OPERAND B 0xFF 0xFF 0xFF 0xFF # | ======================== * | =v8===v9===vA===vB===vC===vD===vE===vF= # | v8 v9 vA vB vC vD vE vF | RESULT 0x12 0x34 0x56 0x77 0xED 0xCB 0xA9 0x88 #################################################################################### : mul32crD vC += vF # Carry add from vD : mul32crC vB += vF # Carry add from vC : mul32crB vA += vF # Carry add from vB : mul32crA v9 += vF # Carry add from vA : mul32cr9 v8 += vF # Carry add from v9 ; : mul32cro # Carry out vD += v7 mul32crD vC += v6 mul32crC vB += v5 mul32crB vA += v6 mul32crA ; : mul32p # Backup operands i := multmp0 save v7 # Multiply matching parts i := multmp0 load v6 v2 := v4 v3 := v5 mul16p v8 := v4 v9 := v5 vA := v6 vB := v7 i := multmp2 load v6 v2 := v4 v3 := v5 mul16p vC := v4 vD := v5 vE := v6 # Do special care for the product at vF, since it's always erased i := mulbkvf v0 := v7 save v0 # Multiply across parts i := multmp2 load v6 mul16p mul32cro i := multmp0 load v6 v2 := v5 v3 := v6 mul16p mul32cro # Restore the vF of the product :next mulbkvf vF := 0 ;
If you find some mistakes, feel free to correct me, I haven't tested the code yet 💀
I'll provide fixed points multiplications out of these.
Any how, you don't need look up table to convert 16-bit fixed points into decimal 😄
The shortest and fastest code for 16-bit fixed points to decimal conversion
that I had come up with would be:
: zeroes 0 0 0 0 0 0 0 0 0 0 0 0 : decimal_result 0 0 0 : decimal_fractional_part 0 0 0 0 0 0 0 0 0 : convert_16_bit_fixed_point_to_decimal # v0 : Hi-byte # v1 : Lo-byte i := decimal_result bcd v0 vF := v1 i := zeroes load v8 v0 := vF # extract decimal of the whole 8-bits decimal_extract_bit decimal_extract_bit decimal_extract_bit decimal_extract_bit decimal_extract_bit decimal_extract_bit decimal_extract_bit decimal_extract_bit # what font index is a dot point v0 := DOT_POINT # store the result i := decimal_fractional_part save v8 return : decimal_extract_bit # performs reverse double-dabble v0 >>= v0 if vF != 0 then v1 += 10 v1 >>= v1 if vF != 0 then v2 += 10 v2 >>= v2 if vF != 0 then v3 += 10 v3 >>= v3 if vF != 0 then v4 += 10 v4 >>= v4 if vF != 0 then v5 += 10 v5 >>= v5 if vF != 0 then v6 += 10 v6 >>= v6 if vF != 0 then v7 += 10 v7 >>= v7 if vF != 0 then v8 += 10 v8 >>= v8 return
Fixed floats, ehm, fixed points, is fractional numbers, which is being stored as integer.
Let's say, in currency, to represent 0.99, just store it as 99; or 1.25, just store it as 125.
Divide them by 100 when you want to display it, or when doing multiplication on them.
And you don't need to divide them when doing addition or subtraction on them.
The same principle applied to binary:
storing 0b1010.101 (10.625) as 0b1010101 (85),
which later divided by 0b1000 (8) since 3 bits are the fraction parts. or
storing 0b111.1111 (7.9375) as 0b1111111 (127),
which is later divided by 0b10000 (16) since 4 bits are the fractions.
In here, you have to determine how much bits you gonna sacrifice to store fractions,
in this case, you gonna have 8 bits integers, 8 bits of fractions, totaling of 16bits number
you gonna have the granularity of 1/256 (0.00390625) which in binary 0b00000000.00000001
and the largest number you can represent with this would be
65535/256 (255.99609375) a.k.a 0b11111111.11111111
Cool,
I had some tricks on my sleeves, for both conversion and arithmetics.
Therefore, would you extend your VM to support 32-bit arithmetics?
I hadn't looked myself into JackVM yet,
and I'm just gonna share what I have, just in case you need it 😄
Implementing 32-bit addition and subtraction is tricky, but, hang in there!
For these routines, you had to arrange your operands as:
########################################################################### # 32-bit, in big-endian e.g v0 v1 v2 v3 v0 v1 v2 v3 # | v0 v1 v2 v3 | OPERAND A 0x12 0x34 0x56 0x78 0x12 0x34 0x56 0x78 # | v4 v5 v6 v7 | OPERAND B 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF # |===============| =v0===v1===v2===v3= + =v0===v1===v2===v3= - # | v0 v1 v2 v3 | RESULT 0x12 0x34 0x56 0x77 0x12 0x34 0x56 0x79 ########################################################################### # 24-bit, in big-endian e.g v0 v1 v2 v0 v1 v2 # | v0 v1 v2 | OPERAND A 0x12 0x34 0x56 0x12 0x34 0x56 # | v4 v5 v6 | OPERAND B 0xFF 0xFF 0xFF 0xFF 0xFF 0xFF # |===============| =v0===v1===v2= + =v0===v1===v2= - # | v0 v1 v2 | RESULT 0x12 0x34 0x55 0x12 0x34 0x57 ########################################################################### # 16-bit, in big-endian e.g v0 v1 v0 v1 # | v0 v1 | OPERAND A 0x12 0x34 0x12 0x34 # | v4 v5 | OPERAND B 0xFF 0xFF 0xFF 0xFF # |===============| =v0===v1= + =v0===v1= - # | v0 v1 | RESULT 0x12 0x33 0x12 0x35 ########################################################################### # 8-bit e.g v0 v0 # | v0 | OPERAND A 0x12 0x12 # | v4 | OPERAND B 0xFF 0xFF # |===============| =v0= + =v0= - # | v0 | RESULT 0x11 0x17 ###########################################################################
This is the whole 32-bits, 24-bits, 16-bits, and 8-bits addition routine within only 24 bytes!
# Carry Operand A : car32 v2 += vF : car24 v1 += vF : car16 v0 += vF ; # Add Operand A by Operand B : add32 v3 += v7 car32 : add24 v2 += v6 car24 : add16 v1 += v5 car16 : add8 v0 += v4 ;
For subtraction, it's another story...
Chip-8's subtraction flag is already stupid, and I couldn't think a way around beside this.
Both subtraction and reversed subtraction, 8-bits, 16-bits, 24-bits, 32-bits, 78 extra bytes!
# Reversed Carry Operand A : ccr32 v2 -= vF : ccr24 v1 -= vF : ccr16 v0 -= vF ; # Decrement Operand A : dec32 v3 -= 1 if v3 == 255 begin : dec24 v2 -= 1 if v2 == 255 begin : dec16 v1 -= 1 if v1 == 255 then : dec8 v0 -= 1 end end ; # Subtraction ( A - B ) : sub32 dec24 v3 -= v7 car32 : sub24 dec16 v2 -= v6 car24 : sub16 dec8 v1 -= v5 car16 : sub8 v0 -= v4 ; # Reversed subtraction ( B - A ) : rsb32 vF := 1 car32 v3 =- v7 crr32 : rsb24 vF := 1 car24 v2 =- v6 crr24 : rsb16 vF := 1 car16 v1 =- v5 crr16 : rsb8 v0 =- v4 ;
Well...
If you want only 32-bit addition / subtraction, they could be simply written as:
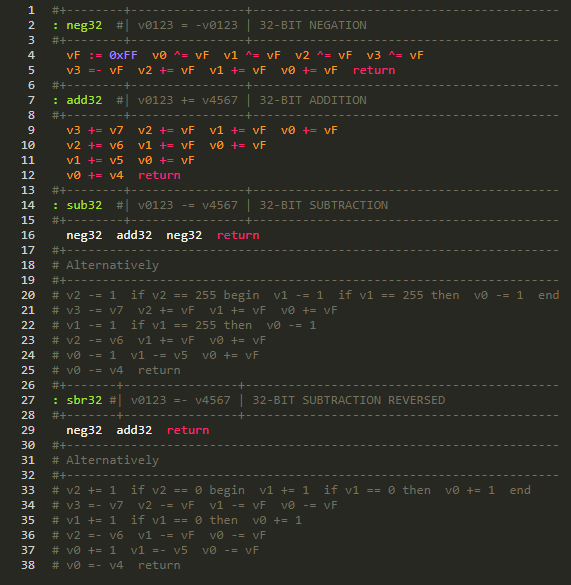
There's still room for improvements for the code I had shown here,
and the redundancies being there is for the sake of readability...
I knew you can optimize it. 😉
Yo, some ideas:
1. Chess game (I'm not up to this, but somebody else can do this one), and maybe with AI for the next level of this hahaha
2. Scrolling platformer, any kind of platformer, but scrolls, would make use of XO-CHIP features for smoother scrolls however
3. Nobody tried Tetris with standard rules here yet (and I'm not up to this)
4. Some sort of complex program that makes use of high level of abstractions, for this case, I'm go with raytracing.
5. Music program (I'll elaborate this later)
Having fixed point arithmetics in CHIP-8 would been good idea haha, it's just way easier to do than doing floating points 👀
And at the same time, not only fixed point, but string conversion of it as well, either fixed point to string or vice versa, just for convenience.
Umm... I'm still unsure how to make this compatible for the ongoing Jack/NAND2Tetris, esp for the string conversion...
I had interest on implementing some sort of arithmetic routines for CHIP-8; either or not uses XO-CHIP extension, but might provide two versions (vanilla and XO-CHIP). I got a dream to have basic raytracing implemented in this system, ignoring on how long it would take to compute, at least without throttling the emulation speed...
Hi, nice to see fellow composer here :)
Are you interested with the 1-bit audio for this system?
It's pretty nice to have others like you to contribute, making chiptunes!
Working for advanced audio in this system might be pretty troublesome, but I had wrote a bit of helpers to make audio programming for this system easy :D
I will post a tutorial on how to produce music for this system here...
You may head up here (XO-Tracker), and see what the XO-CHIP's sound system is capable of.
Multi-voiced and multi-channel audio capability test
https://kouzeru.github.io/Octo/index.html?key=Cn39wl5y
[ZXCV to mute individual voice, ASDF to unmute]
Hey, I'm fascinated about this expansion of XO-Chip! We'd like to discuss about this more, would you interested join into the Emulation Development discord server? There's might be a lot to be talked there https://discord.gg/dkmJAes ;)







