While working on the gamepad input module for Turtle Engine, I found a need for having the input value from a joystick be snapped to the nearest cardinal or intercardinal (45deg angle). Since I like math, and hopefully you do as well, I thought I'd write up a quick post on how to do this and the math behind it. Maybe someone will find this useful 😅

💡 Note While I will be going over the math, I will also be presenting the code written for this. The presented code is in C# but should be easily translated to whatever language you prefer.

The Problem

Let's state the problem before figuring out the solution. The problem currently is that given any Vector2 input from a gamepad joystick, where the x and y elements range from -1.0f to 1.0f, we want to snap this Vector2 value to the nearest 45 degree. Ideally, we would want to retain the length of the Vector2 on whatever angle it snaps too.

Let's start with an example scenario that we can work with

In this example, the thumbstick is being pushed up and to the right.  Let's say the value being returned back is (0.4, 0.7).  The value isn't important, but maybe it'll help with visualizing(?).

Solving

First, let's represent the Vector2 value as a right triangle, like the following image.

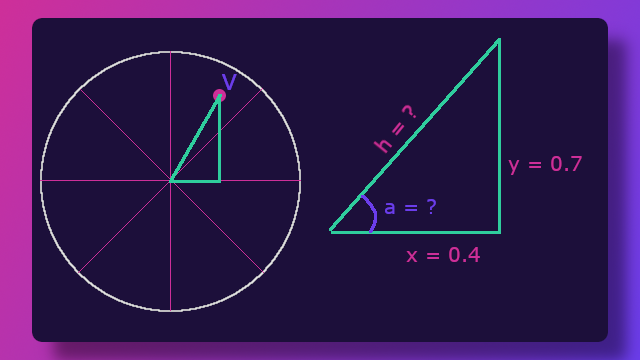
From here, there are two values that we need to first calculate from this; the hypotenuse and the angle of the Vector2. The hypotenuse can be calculated using good ol' Pythagorean's Therom a² * b² = c² where a = the base of the triangle, b = the side of the triangle, and c = the hypotenuse. Since we are solving for the hypotenuse, we solve for c by doing c = √(a² * b²). Knowing the hypotenuse tells use the length of the Vector2. We'll need this for later.

To get the angle of the Vector2, we can use the atan2 function. atan2 will give us the angle of a Vector2, in radians, measured from the positive x-axis rotating counterclockwise.

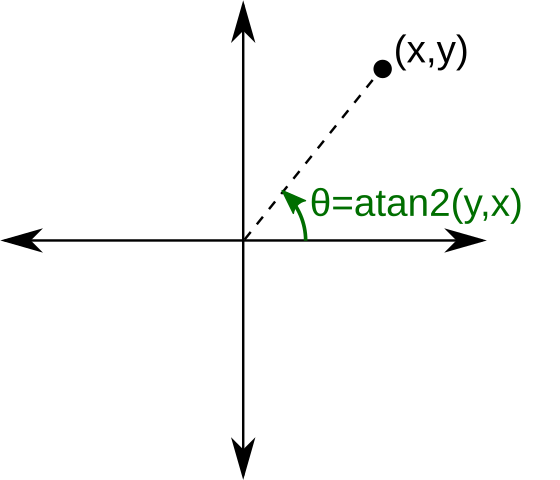
To do this, we use the formula angle=atan2(y, x). Note the y is before the x here when using this function. It's also important to note that we'll be dealing in radians going forward.

Now that we know this, we can start building our method out. Let's create the method and add the calculations for these two values of the given Vector2.

public Vector2 Snap(Vector2 v) 
{
     //  Get the angle of the given vector
     float angle = (float)Math.Atan2(v.Y, v.X);

     //  Get the hypotenuse (length) of the given vector
     float hypotenuse = (float)Math.Sqrt((v.X * v.X) + (v.Y * v.Y));

     // ... the rest to be added as we go through this 
}

Now that we have the angle and length of the Vector2, the next step is to figure out what the closest cardinal or intercardinal angle is to the angle of the Vector2. Cardinals and intercardinals will be at every 45 degree angle. However, from the atan2 function as well as upcoming ones, we'll need to deal in radians. So first, we need to be able to express 45 degrees as radians. To convert degrees to radians we multiply the deg by PI/180 or g(d) = d * (PI / 180) where d is the angle in degrees.

Then, to determine the nearest cardinal or intercardinal to snap to, can use the following formula g(a, n) = round(a / n) * n where a is the angle and n is the 45 degrees in radians. So let's add this to our method, which will give us the following now.

public Vector2 Snap(Vector2 v) 
{
     //  Get the angle of the given vector
     float angle = (float)Math.Atan2(v.Y, v.X);

     //  Get the hypotenuse (length) of the given vector
     float hypotenuse = (float)Math.Sqrt((v.X * v.X) + (v.Y * v.Y));

     // Convert 45degress to radians
     float rad45 = (float)(45 * (Math.PI / 180));

     //  Determine the nearest cardinal/intercardinal angle to snap to
     float snapTo = (float)Math.Round(angle / rad45) * rad45;

      // ... the rest to be added as we go through this 
}

Now that we have the new angle to snap to and the length of the original vector, we have all the information we need to calculate the new x and y coordinates. So how do we do that? Well, take a look at the following image.

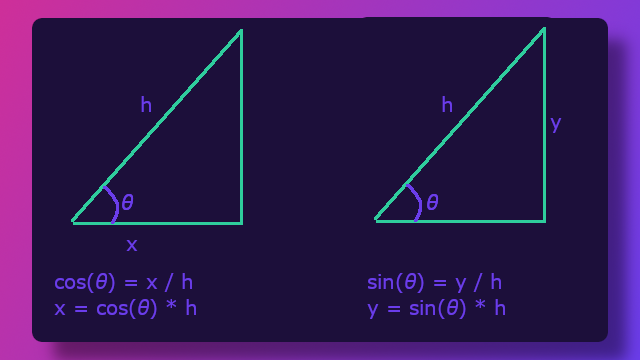
cosine of an angle is the ratio to the side adjacent to the angle and the hypotenuse. Or plainly put, it is equal to the adjacent side x divided by the hypotenuse. sine of an angle on the other hand is the ratio of the side opposite the angle and the hypotenuse, or opposite side y divided by the hypotenuse.

Since we already know the hypotenuse when we calculated the length of the Vector earlier, and we already know the angle when we discovered the nearest angle to snap to, we just need to modify the two formulas to now solve for x and y. Doing that gives us x=cos(θ) * h and y=sin(θ) * h. So by adding this into our function, we can calculate what the new x and y coordinates will be for the Vector2 once it has snapped to the new angle.

So to complete our function, it would look like this

public Vector2 Snap(Vector2 v) 
{
     //  Get the angle of the given vector
     float angle = (float)Math.Atan2(v.Y, v.X);

     //  Get the hypotenuse (length) of the given vector
     float hypotenuse = (float)Math.Sqrt((v.X * v.X) + (v.Y * v.Y));

     // Convert 45degress to radians
     float rad45 = (float)(45 * (Math.PI / 180));

     //  Determine the nearest cardinal/intercardinal angle to snap to
     float snapTo = (float)Math.Round(angle / rad45) * rad45;

     Vector2 snappedVector = new();

     // Calculate the x of the vector from the snapped angle
     snappedVector.X = (float)(Math.Cos(snapTo) * hypotenuse);

     //  Calculate the y of the vector from the snapped angle
     snappedVector.Y = (float)(Math.Sin(snapTo) * hypotenuse);

     return snappedVector; 
}

And that's it. Math is fun right? 😬